[통계] 기술 통계: 데이터 요약, 표본 추출, 확률 분포, 표본 분포

해당 포스트는 노션의 코드를 가져와 작성하여 일부 깨짐이 있습니다. 온전한 글은 아래 첨부한 페이지 링크에 오셔서 확인 가능합니다 :) 빅데이터 분석기사를 준비하며 통계 기법에 대해 간략히 정리한 페이지 입니다.

https://www.notion.so/monamienamie/Chapter3-eae26485f8404cd881069506befd9108

Chapter3. 통계 기법 이해

간단한 계산은 문제로 나올 수 있으니 일부 손풀이 가능한 공식은 숙지할 것!

기술통계

• 기술통계는 데이터 분석의 목적으로 수집된 데이터를 확률 · 통계적으로 정리 · 요약하는 기초적인 통계이다.

• 기술통계는 분석의 초기 단계에서 데이터 분포의 특징을 파악하려는 목적으로 산출한다.

데이터 요약

대푯값

주어진 자료 전체에서 중심 위치를 나타내는 값

평균값(Average)

• 자료를 모두 더한 후 자료 개수로 나눈 값

• 평균값은 전부 같은 가중치를 두며 이상값에 민감하다.

평균의 종류
모평균
표본평균

중위수(Median)

• 모든 데이터 값을 오름차순으로 순서대로 정렬하였을 때, 중앙에 위치한 값이다.

• 중위수는 이상치의 영향을 받지 않는다.

$$d_{median} = {n+1 \over 2}$$

n = 데이터의 개수

• 중위수는 데이터 값의 수가 홀수일 경우에는 중위수가 하나가 되지만, 데이터 값의 수가 짝수일 경우에는 중앙에 있는 두 개의 값을 평균으로 하여 정한다.

최빈수(Mode)

• 데이터 값 중에서 빈도수가 가장 높은 데이터 값

• 관측된 데이터 값 중에서 가장 여러 번 나타난 값

사분위수(Quartile)

• 모든 데이터 값을 순서대로 배열하였을 때, 4등분한 지점에 있는 값

제1 사분위수	데이터를 오름차순 했을 때 첫 번째 사등분 점
제2 사분위수 (= 중위수_)	데이터를 오름차순 했을 때 두 번째 사등분 점
3 사분위수	데이터를 오름차순 했을 때 세 번째 사등분 점

산포도

주어진 자료가 흩어진 정도

분산(Variance)

• 데이터가 평균으로부터 얼마나 떨어져 있는 지를 나타내는 값

• 양의 편차와 음의 편차를 더하면 0이 될 수 있으므로 각 데이터 값을 제곱 후 모두 더한다.

분산의 종류
모분산
표본 분산

표준편차(Standard Deviation)

분산에 양의 제곱근을 취한 값

표준편차의 종류
모 표준편차
표본 표준편차

범위(Range)

자료 중에서 최댓값과 최솟값의 차이

$$R = X_{max} - X_{min}$$

$X_{max}$ : 최대 데이터 값

$X_{min}$ : 최소 데이터 값

IQR(사분 범위, 사분위수 범위)

제3 사분위 수와 제1 사분위 수의 차이 값

$$IQR = Q_3 - Q_1$$

사분편차(Quartile Deviation)

제3 사분위 수와 제1 사분위 수의 차이인 IQR의 절반 값

$$IQR = {Q_3 - Q_1 \over 2}$$

변동계수(=변이계수; CV)

• 표준편차를 평균으로 나눈 값

• 측정 단위가 서로 다른 자료의 흩어진 정도를 상대적으로 비교할 때 사용한다.

데이터 분포

데이터 분포의 형태와 대칭성을 설명할 수 있는 통계량

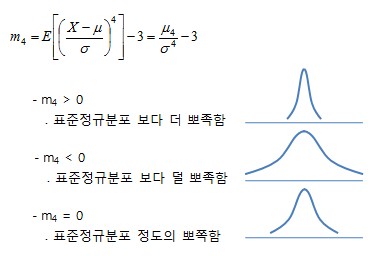
첨도(Kurtosis)

출처: 정보통신기술용어해설 copyright by cha jae-bok

왜도(Skewness)

출처: 오빠두엑셀 https://www.oppadu.com/엑셀-skew-함수/

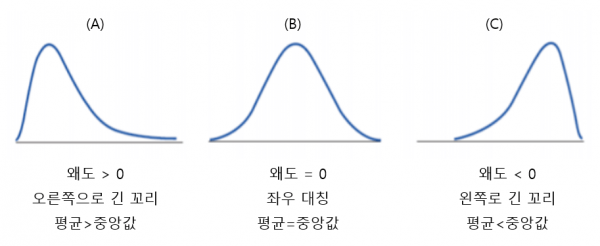
왜도>0	우측으로 긴 꼬리 최빈수 < 중위수 < 평균
왜도=0	좌우대칭 최빈수 = 중위수 = 평균
왜도<0	좌측으로 긴 꼬리 최빈수>중위수>평균

공분산

두 개의 변수 사이의 관련성을 나타내는 통계량

공분산 종류
모공분산
표본공분산

공분산의 해석

Cov > 0	두 개의 변수 중 하나의 값이 상승하는 경향을 보일 때 다른 값도 상승하는 경향을 보인다면, 공분산의 값은 양수가 됨
Cov < 0	두 개의 변수 중 하나의 값이 상승하는 경향을 보일 때 다른 값이 하강하는 경향을 보인다면, 공분산의 값은 음수가 됨

• 상관관계의 상승 또는 하강하는 경향을 이해할 수 있다.

• 공분산 값의 크기는 측정 단위에 따라 달라지므로 선형관계의 강도를 나타내지는 못한다.

상관관계

• 두 변수 사이에 선형 또는 비선형적 관계가 있는지를 분석하는 방법

• 인과관계는 알 수 없음!

분류

단순 상관 분석	두 개의 변수 사이의 상관성 분석
다중 상관 분석	세 개 이상의 변수 사이의 상관성 분석

⭐변수의 속성에 따른 상관관계 분류

변수 속성		분석 방법
수치형 데이터	• 등간 척도, 비율 척도에 해당하는 수치형 데이터 (키, 몸무게, 나이 등) • 변수 간 연산이 가능	피어슨 상관계수
순서 데이터	• 범주형 데이터 중 순서적 데이터 • 데이터의 순서에 의미 (1등, 2등..) • 변수 간 연산 불가능 (1등 + 2등 ≠ 3등)	스피어만 상관계수
명목적 데이터	• 범주형 데이터 중 명목척도 • 데이터의 특성을 구분하기 위한 숫자나 기호 (성별, 1반, 2반…) • 변수 간 연산 불가능 (1반 + 2반 ≠ 3반)	카이제곱 검정 (교차 분석)

상관계수

Correlation Coefficient

• 두 변수 사이의 연관성을 수치로 객관화하여 두 변수 사이의 방향성과 강도를 표현하는 방법

상관계수의 해석

-1 ~ +1의 값을 가진다. (음의 상관관계 ~ 양의 상관관계)

출처: 정보통신기술용어해설 http://www.ktword.co.kr/index.php

표본추출

• 모집단의 일부를 일정한 방법에 따라 표본으로 선택하는 과정

표본 추출의 종류

단순 무작위 추출	• 정해진 규칙 없이 표본을 추출 • 표본의 크기가 커질수록 정확도가 높아지며, 추정값이 모수에 근접하므로 추정 값의 분산이 줄어든다
계통 추출	• 모집단을 일정한 간격으로 추출
층화 추출	• 모집단을 여러 계층으로 나누고, 계층별로 무작위 추출을 수행하는 방식 • 층내는 동질적이고, 층간은 이질적이다
군집 추출	• 모집단을 여러 군집으로 나누고, 일부 군집의 전체를 추출하는 방식 • 집단 내부는 이질적이고, 집단 외부는 동질적이다.

확률분포

확률 및 기본 통계 이론

확률

비슷한 현상이 반복해서 일어날 경우에 어떤 사건이 발생할 가능성을 0 ~ 1 의 값으로 나타낸 것

확률의 계산

$$P(A) = {n_A \over n_B} = {A의개수 \over S의개수}$$

$S$: 표본 공간 ⇒ 전체 개수

$A$: 사건 ⇒ 측정하려는(관심 있는) 부분

교사건

A와 B가 동시에 속하는 결과들의 모임

$P(A\cap B)$ 교집합

조건부 확률

• 어떤 사건이 일어난다는 조건에서 다른 사건이 일어날 확률

• 두 개의 사건 A와 B에 대하여 사건 A가 일어난다는 선행 조건 하에 사건 B가 일어날 확률

사건 A가 일어났을 때 사건 B가 일어날 조건부 확률	$P(B|A) = {P(A\cap B) \over P(A)}, P(A)\neq 0$
사건 B가 일어났을 때 사건 A가 일어날 조건부 확률	$P(A|B) = {P(A \cap B) \over P(B)}, P(B) \neq 0$ 조건부 확률 식

베이즈 정리

• 어떤 사건에 대해 관측 전(사전 확률) 원인에 대한 가능성과 관측 후(사후 확률) 원인 가능성 사이의 관계를 설명하는 확률 이론

• 어떤 사건 B가 서로 배반인 A1, A2, A3 … An중 어느 한 가지 경우로 발생하는 경우 실제 B가 일어날 때, Ai가 발생할 확률

e.g. 어떤 회사의 A공장의부품은 50%를 생산하고 불량률은 1%이다. B공장은 부품을 30% 생산하고 불량률은 2%이고, C공장은 부품을 20% 생산하고 불량률은 3%이다. 부품을 선택했을 때 (사전 확률) C공장에서 생산한 부품일 확률을 구하시오.

A1: A공장, A2: B공장, A3: C공장, B: 불량률

P(A1): A공장에서 부품을 생산할 확률(50%), P(B|A1): A공장에서의 불량률(1%)
P(A2): B공장에서 부품을 생산할 확률(30%), P(B|A2): B공장에서의 불량률(2%)
P(A3): C공장에서 부품을 생산할 확률(20%), P(B|A3): C공장에서의 불량률(3%)
P(A3|B): 불량품이 C공장에서 생산될 확률

$\begin{matrix}P(A_3|B) &=& {P(A_3)P(B|A_3) \over P(A_1)P(B|A_1) + P(A_2)P(B|A_2) + P(A_3)P(B|A_3)} &=& 20 \times 3 \over 50 \times 1 + 30 \times 2 + 20 \times 3 &=&60 \over 50 +60+60 &=&6 \over 17 \end{matrix}$약 35%

확률분포 및 확률변수

확률분포

• 확률변수가 특정한 값을 가질 확률을 나타내는 분포

• 이산확률분포, 연속확률분포

이산확률분포

• 이산확률변수(셀 수 있는 것: 개수 등) X가 가지는 확률 분포

종류	설명
포아송 분포	이산형 확률 분포 중 주어진 시간 또는 영역에서 어떤 사건의 발생 횟수를 나타내는 확률분포
베르누이 분포	특정 실험의 결과가 성공 또는 실패 (1 또는 0) 두 가지 결과 중 하나를 얻는 확률분포
이항 분포	n번의 시행 중 각 시행의 확률이 p일 때, k번 성공할 확률분포

확률 질량 함수(PMF)

• 이산확률변수에서 특정 값에 대한 확률을 나타내는 함수

특징

성질	설명
모든 x에 대해 f(x) ≥ 0	모든 확률은 0보다 큼
$\sum_{x=-\infty}^\infty f(x) = 1$	모든 확률을 합치면 1
$P(a \le X \le b) = \sum_{x=a}^bf(x)$	a와 b 사이의 확률은 a에서 b까지의 확률을 합한 것과 같음

누적 질량 함수(CMF)

• 이산확률변수가 특정 값보다 작거나 같을 확률

연속확률분포

• 확률변수 X가 실수와 같이 연속적인 값을 취할 때 이를 연속확률변수라하고 이러한 연속확률변수 X가 가지는 확률 분포

• 정규분포, 표준정규분포, t-분포, 지수분포, chi-square분포, F-분포 등

종류	설명
졍규분포	종 모양의 분포
표준정규분포	• 표본 통계량이 표본 평균일 때 이를 표준화(정규화)시킨 표본분포 • 정규분포를 해석할 때 많이 쓰임 • 평균(기댓값)은 0 표준 편차(분산)는 1
t-분포	• 모집단이 정규분포라는 정도만 알고 모표준편차는 모를 때 모집단의 평균을 추론하는 분포 • 소표본에 사용 • 표본의 크기가 충분히 클 경우 중심극한정리에 의해 정규분포를 따른다 • 정규분포의 평균의 해석에 많이 쓰이는 분포 • 정규분포를 따르는 두 집단 간의 평균 차이 등 • 자유도가 30이 넘으면 표준정규분포와 비슷해지고, 자유도가 증가할수록 표준정규분포에 가까워짐
지수분포	• 지정된 시점으로부터 어떤 사건이 일어날대까지 걸리는 시간을 측정하는 확률 분포
카이제곱분포	• 표본통계량이 표본분산일 때의 표본분포 • n개의 서로 독립적인 표준 정규 확률변수를 각각 제곱한 다음 합해서 얻어지는 분포 • 자유도 n이 작을수록 왼쪽으로 치우치는 비대칭적 모양이다
F-분포	• 모집단 분산이 서로 동일하다고 가정되는 두 모집단으로부터 표본 크기가 각각 n1, n2인 독립적인 두 개의 표본을 추출하였을때 두 개의 표본분산 s1, s2의 비율 • 독립적인 chi-sqaure 분포가 있을 때, 두 확률변수의 비

확률밀도함수(PDF)

• 연속확률변수의 분포를 나타내는 함수

성질

• 모든 확률은 0보다 크다

• 모든 확률을 합치면 1이다

누적밀도함수(CDF)

• 연속확률변수가 특정 값보다 작거나 같을 확률을 나타내는 함수

성질

• 함숫값은 점점 증가한다

• x값이 $-\infty$ 이면 0, +$\infty$이면 1

최대우도법

• 어떤 확률변수에서 표집한 값들을 토대로 그 확률변수의 모수를 구하는 방법

• 어떤 모수가 주어졌을 때, 원하는 값들이 나올 가능도를 최대로 만드는 모수를 선택하는 방법, 점추정 방식

확률변수

• 특정 확률로 발생하는 결과를 수치적 값으로 표현하는 변수

• 확률에 의해 그 값이 결정되는 변수

앞면의 수(X)	0	1	2	계
확률	1/4	1/2	1/4	1

• 이산확률변수, 연속확률변수

기댓값

• 확률변수의 값에 해당하는 확률을 곱하여 모두 더한 값

• 확률변수의 평균과 같음

• 해당 확률분포에서 평균적으로 기대할 수 있는 값이며, 해당 확률분포의 중심 위치를 설명해주는 값

분산

• 두 확률 분포의 공분산 공식

$$Cov (X,Y) = \sigma_{XY} = E(XY) -E(X)E(Y)$$

체비셰프정리

• 임의의 양수 k에 대하여 확률변수가 평균으로부터 k배의 표준 편차 범위 내에 있을 확률에 대한 예측값을 보수적으로 제공하는 정리

• 관측값들의 분포에 상관 없이 성립하지만, 확률에 대한 하한값 정도만 제공해줄 수 있음

표본 분포

모집단에서 추출한 일정한 개수의 표본에 대한 분포 상태

표본집단 통계량으로 모집단을 추정

모집단과 표본

• 모집단: 연구의 관심이 되는 집단 전체

• 표본: 특정 연구에서 선택된 모집단의 부분 집합

• 표집: 모집단에서 표본을 추출하는 절차 (표본 추출)

모수 population parameter

• 파라미터: 어떤 시스템의 특성을 나타내는 값

• 모수: 모집단population의 파라미터 (즉, 모집단의 특성을 나타내는 값: 모평균, 모분산..)

통계량 sample statistic

:표본에서 얻어진 수로 계산한 값 (=통계치) 표본평균, 표본분산..

• 추론 통계: 표본 통계량을 일반화하여 모집단에 대해 추론하는 것

표집분포

: 통계량의 확률의 분포

특징

1. 각 표본의 분포는 모집단의 분포와 비슷

2. 표집 분포는 모수를 중심으로, 모수와 가까운 값이 더 많이 나옴

3. 어떤 통계량은 표집 분포의 형태를 이론적으로 알 수 있음

추정 estimation

: 통계량으로부터 모수를 추론하는 것

• 점 추정: 하나의 수치로 추정

• 구간 추정: 구간으로 추정

신뢰 구간 confidence interval

대표적인 구간 추정 방법

신뢰구간 = 통계량 ∓ 오차범위

신뢰 수준 confidence level

: 신뢰구간에 모수가 존재하는 표본의 비율

• 신뢰 수준을 높인다는 것 → 예외를 인정하지 않는다! → 표본의 범위가 너무 넓어짐

• 신뢰 수준이 낮다 → 표본이 적어짐 (극단적인 경우는 쳐냄)

따라서, 95%, 99% 정도를 추천하지만 절대적인 기준은 없음

그러니까, 신뢰수준이 높을 수록 정확한 결과라고 할 수 없음